mirror of
https://github.com/massbug/judge4c.git
synced 2025-05-17 14:56:36 +00:00
1106 lines
29 KiB
TypeScript
1106 lines
29 KiB
TypeScript
import { PrismaClient, Prisma, EditorLanguage, LanguageServerProtocol } from "@/generated/client";
|
|
|
|
const prisma = new PrismaClient();
|
|
|
|
const editorLanguageConfigData: Prisma.EditorLanguageConfigCreateInput[] = [
|
|
{
|
|
language: EditorLanguage.c,
|
|
label: "C",
|
|
fileName: "main",
|
|
fileExtension: ".c",
|
|
languageServerConfig: {
|
|
create: {
|
|
protocol: LanguageServerProtocol.ws,
|
|
hostname: "localhost",
|
|
port: 4594,
|
|
path: "/clangd",
|
|
},
|
|
},
|
|
dockerConfig: {
|
|
create: {
|
|
image: "gcc",
|
|
tag: "latest",
|
|
workingDir: "/src",
|
|
compileOutputLimit: 1 * 1024 * 1024,
|
|
runOutputLimit: 1 * 1024 * 1024,
|
|
},
|
|
},
|
|
},
|
|
{
|
|
language: EditorLanguage.cpp,
|
|
label: "C++",
|
|
fileName: "main",
|
|
fileExtension: ".cpp",
|
|
languageServerConfig: {
|
|
create: {
|
|
protocol: LanguageServerProtocol.ws,
|
|
hostname: "localhost",
|
|
port: 4595,
|
|
path: "/clangd",
|
|
},
|
|
},
|
|
dockerConfig: {
|
|
create: {
|
|
image: "gcc",
|
|
tag: "latest",
|
|
workingDir: "/src",
|
|
compileOutputLimit: 1 * 1024 * 1024,
|
|
runOutputLimit: 1 * 1024 * 1024,
|
|
},
|
|
},
|
|
},
|
|
];
|
|
|
|
const userData: Prisma.UserCreateInput[] = [
|
|
{
|
|
name: "cfngc4594",
|
|
email: "cfngc4594@gmail.com",
|
|
password: "$2b$10$edWXpq2TOiiGQkPOXWKGlO4EKnp2YyV7OoS2qqk/W0E6GyiVQIC66",
|
|
role: "ADMIN",
|
|
problems: {
|
|
create: [
|
|
{
|
|
displayId: 1000,
|
|
title: "Two Sum",
|
|
description: `Given an array of integers \`nums\` and an integer \`target\`, return indices of the two numbers such that they add up to \`target\`.
|
|
|
|
You may assume that each input would have **exactly one solution**, and you may not use the same element twice.
|
|
|
|
You can return the answer in any order.
|
|
|
|
<VideoEmbed platform="bilibili" id="BV1TC411b7H8" />
|
|
|
|
## Examples
|
|
|
|
### Example 1
|
|
|
|
\`\`\`shell
|
|
Input: nums = [2,7,11,15], target = 9
|
|
Output: [0,1]
|
|
Explanation: Because nums[0] + nums[1] == 9, we return [0, 1].
|
|
\`\`\`
|
|
|
|
### Example 2
|
|
|
|
\`\`\`shell
|
|
Input: nums = [3,2,4], target = 6
|
|
Output: [1,2]
|
|
\`\`\`
|
|
|
|
### Example 3
|
|
|
|
\`\`\`shell
|
|
Input: nums = [3,3], target = 6
|
|
Output: [0,1]
|
|
\`\`\`
|
|
|
|
## Constraints
|
|
|
|
\`\`\`math
|
|
2 <= nums.length <= 10^4
|
|
\`\`\`
|
|
|
|
\`\`\`math
|
|
-10^9 <= nums[i] <= 10^9
|
|
\`\`\`
|
|
|
|
\`\`\`math
|
|
-10^9 <= target <= 10^9
|
|
\`\`\`
|
|
|
|
<div align="center">
|
|
Only one valid answer exists.
|
|
</div>
|
|
|
|
**Follow-up:** Can you come up with an algorithm that is less than $O(n^2)$ time complexity?
|
|
|
|
---
|
|
|
|
<Accordion title="Hint 1">
|
|
A really brute force way would be to search for all possible pairs of numbers but that would be too slow. Again, it's best to try out brute force solutions for just for completeness. It is from these brute force solutions that you can come up with optimizations.
|
|
</Accordion>
|
|
|
|
<Accordion title="Hint 2">
|
|
So, if we fix one of the numbers, say \`x\`, we have to scan the entire array to find the next number \`y\` which is \`value - x\` where value is the input parameter. Can we change our array somehow so that this search becomes faster?
|
|
</Accordion>
|
|
|
|
<Accordion title="Hint 3">
|
|
The second train of thought is, without changing the array, can we use additional space somehow? Like maybe a hash map to speed up the search?
|
|
</Accordion>`,
|
|
solution: `<VideoEmbed platform="youtube" id="tSI98g3PDyE" />
|
|
|
|
## Approach 1: Brute Force
|
|
|
|
### Algorithm
|
|
|
|
The brute force approach is simple. Loop through each element $x$ and find if there is another value that equals to $target - x$.
|
|
|
|
### Implementation
|
|
|
|
\`\`\`c showLineNumbers
|
|
int* twoSum(int* nums, int numsSize, int target, int* returnSize) {
|
|
for (int i = 0; i < numsSize; i++) {
|
|
for (int j = i + 1; j < numsSize; j++) {
|
|
if (nums[j] == target - nums[i]) {
|
|
int* result = malloc(sizeof(int) * 2);
|
|
result[0] = i;
|
|
result[1] = j;
|
|
*returnSize = 2;
|
|
return result;
|
|
}
|
|
}
|
|
}
|
|
// Return an empty array if no solution is found
|
|
*returnSize = 0;
|
|
return malloc(sizeof(int) * 0);
|
|
}
|
|
\`\`\`
|
|
|
|
### Complexity Analysis
|
|
|
|
- **Time complexity:** $O(n^2)$.
|
|
|
|
For each element, we try to find its complement by looping through the rest of the array which takes $O(n)$ time. Therefore, the time complexity is $O(n^2)$.
|
|
|
|
- **Space complexity:** $O(1)$.
|
|
|
|
The space required does not depend on the size of the input array, so only constant space is used.
|
|
|
|
---
|
|
|
|
## Approach 2: Two-pass Hash Table
|
|
|
|
### Intuition
|
|
|
|
To improve our runtime complexity, we need a more efficient way to check if the complement exists in the array. If the complement exists, we need to get its index. What is the best way to maintain a mapping of each element in the array to its index? A hash table.
|
|
|
|
We can reduce the lookup time from $O(n)$ to $O(1)$ by trading space for speed. A hash table is well suited for this purpose because it supports fast lookup in near constant time. I say "near" because if a collision occurred, a lookup could degenerate to $O(n)$ time. However, lookup in a hash table should be amortized $O(1)$ time as long as the hash function was chosen carefully.
|
|
|
|
### Algorithm
|
|
|
|
A simple implementation uses two iterations. In the first iteration, we add each element's value as a key and its index as a value to the hash table. Then, in the second iteration, we check if each element's complement ($target - nums[i]$) exists in the hash table. If it does exist, we return current element's index and its complement's index. Beware that the complement must not be $nums[i]$ itself!
|
|
|
|
### Implementation
|
|
|
|
\`\`\`c showLineNumbers
|
|
int* twoSum(int* nums, int numsSize, int target, int* returnSize) {
|
|
struct hashTable {
|
|
int key;
|
|
int value;
|
|
UT_hash_handle hh;
|
|
} *hashTable = NULL, *item, *tmpItem;
|
|
|
|
for (int i = 0; i < numsSize; i++) {
|
|
HASH_FIND_INT(hashTable, &nums[i], item);
|
|
if (item) {
|
|
int* result = malloc(sizeof(int) * 2);
|
|
result[0] = item->value;
|
|
result[1] = i;
|
|
*returnSize = 2;
|
|
HASH_ITER(hh, hashTable, item, tmpItem) {
|
|
HASH_DEL(hashTable, item);
|
|
free(item);
|
|
}
|
|
return result;
|
|
}
|
|
item = malloc(sizeof(struct hashTable));
|
|
item->key = target - nums[i];
|
|
item->value = i;
|
|
HASH_ADD_INT(hashTable, key, item);
|
|
}
|
|
|
|
HASH_ITER(hh, hashTable, item, tmpItem) {
|
|
HASH_DEL(hashTable, item);
|
|
free(item);
|
|
}
|
|
|
|
*returnSize = 0;
|
|
// If no valid pair is found, return an empty array
|
|
return malloc(sizeof(int) * 0);
|
|
}
|
|
\`\`\`
|
|
|
|
### Complexity Analysis
|
|
|
|
- **Time complexity:** $O(n)$.
|
|
|
|
We traverse the list containing $n$ elements exactly twice. Since the hash table reduces the lookup time to $O(1)$, the overall time complexity is $O(n)$.
|
|
|
|
- **Space complexity:** $O(n)$.
|
|
|
|
The extra space required depends on the number of items stored in the hash table, which stores exactly $n$ elements.
|
|
|
|
---
|
|
|
|
## Approach 3: One-pass Hash Table
|
|
|
|
### Algorithm
|
|
|
|
It turns out we can do it in one-pass. While we are iterating and inserting elements into the hash table, we also look back to check if current element's complement already exists in the hash table. If it exists, we have found a solution and return the indices immediately.
|
|
|
|
### Implementation
|
|
|
|
\`\`\`c showLineNumbers
|
|
int* twoSum(int* nums, int numsSize, int target, int* returnSize) {
|
|
struct hashTable {
|
|
int key;
|
|
int value;
|
|
UT_hash_handle hh;
|
|
} *hashTable = NULL, *item;
|
|
|
|
for (int i = 0; i < numsSize; i++) {
|
|
int complement = target - nums[i];
|
|
HASH_FIND_INT(hashTable, &complement, item);
|
|
if (item) {
|
|
int* result = malloc(sizeof(int) * 2);
|
|
result[0] = item->value;
|
|
result[1] = i;
|
|
*returnSize = 2;
|
|
HASH_CLEAR(hh, hashTable); // Free the hash table
|
|
return result;
|
|
}
|
|
item = malloc(sizeof(struct hashTable));
|
|
item->key = nums[i];
|
|
item->value = i;
|
|
HASH_ADD_INT(hashTable, key, item);
|
|
}
|
|
|
|
*returnSize = 0;
|
|
HASH_CLEAR(hh, hashTable); // Free the hash table
|
|
// Return an empty array if no solution is found
|
|
return malloc(0); // Allocate 0 bytes
|
|
}
|
|
\`\`\`
|
|
|
|
### Complexity Analysis
|
|
|
|
- **Time complexity:** $O(n)$.
|
|
|
|
We traverse the list containing $n$ elements only once. Each lookup in the table costs only $O(1)$ time.
|
|
|
|
- **Space complexity:** $O(n)$.
|
|
|
|
The extra space required depends on the number of items stored in the hash table, which stores at most $n$ elements.
|
|
|
|
---
|
|
|
|
## Summary of Approaches
|
|
|
|
| Approach | Time Complexity | Space Complexity |
|
|
| ------------------- | :-------------: | :--------------: |
|
|
| Brute Force | $O(n^2)$ | $O(1)$ |
|
|
| Two-pass Hash Table | $O(n)$ | $O(n)$ |
|
|
| One-pass Hash Table | $O(n)$ | $O(n)$ |`,
|
|
difficulty: "EASY",
|
|
published: true,
|
|
templates: {
|
|
create: [
|
|
{
|
|
language: "c",
|
|
template: `#include <stdio.h>
|
|
#include <stdlib.h>
|
|
#include <string.h>
|
|
|
|
/**
|
|
* Note: The returned array must be malloced, assume caller calls free().
|
|
*/
|
|
int *twoSum(int *nums, int numsSize, int target, int *returnSize) {
|
|
|
|
}
|
|
|
|
int *parseIntArray(char *line, int *len) {
|
|
line[strcspn(line, "\\n")] = 0;
|
|
char *p = line;
|
|
while (*p && (*p == '[' || *p == ' ' || *p == ']'))
|
|
p++;
|
|
|
|
int capacity = 10;
|
|
int *arr = malloc(capacity * sizeof(int));
|
|
*len = 0;
|
|
|
|
char *token = strtok(p, ",");
|
|
while (token) {
|
|
if (*len >= capacity) {
|
|
capacity *= 2;
|
|
arr = realloc(arr, capacity * sizeof(int));
|
|
}
|
|
arr[(*len)++] = atoi(token);
|
|
token = strtok(NULL, ",");
|
|
}
|
|
return arr;
|
|
}
|
|
|
|
char *formatOutput(int *res, int resLen) {
|
|
if (resLen == 0)
|
|
return "[]";
|
|
|
|
char *buf = malloc(resLen * 12 + 3);
|
|
char *p = buf;
|
|
*p++ = '[';
|
|
for (int i = 0; i < resLen; i++) {
|
|
p += sprintf(p, "%d", res[i]);
|
|
if (i != resLen - 1)
|
|
*p++ = ',';
|
|
}
|
|
*p++ = ']';
|
|
*p = 0;
|
|
return buf;
|
|
}
|
|
|
|
int main() {
|
|
char line[1024];
|
|
while (fgets(line, sizeof(line), stdin)) {
|
|
int numsSize;
|
|
int *nums = parseIntArray(line, &numsSize);
|
|
|
|
if (!fgets(line, sizeof(line), stdin))
|
|
break;
|
|
int target = atoi(line);
|
|
|
|
int returnSize;
|
|
int *res = twoSum(nums, numsSize, target, &returnSize);
|
|
|
|
char *output = formatOutput(res, returnSize);
|
|
printf("%s\\n", output);
|
|
|
|
free(nums);
|
|
if (returnSize > 0)
|
|
free(res);
|
|
if (returnSize > 0)
|
|
free(output);
|
|
}
|
|
return 0;
|
|
}`,
|
|
},
|
|
{
|
|
language: "cpp",
|
|
template: `#include <iostream>
|
|
#include <sstream>
|
|
#include <string>
|
|
#include <vector>
|
|
|
|
using namespace std;
|
|
|
|
class Solution {
|
|
public:
|
|
vector<int> twoSum(vector<int> &nums, int target) {
|
|
|
|
}
|
|
};
|
|
|
|
vector<int> parseIntArray(const string &input) {
|
|
vector<int> result;
|
|
string trimmed = input.substr(1, input.size() - 2);
|
|
stringstream ss(trimmed);
|
|
string token;
|
|
|
|
while (getline(ss, token, ',')) {
|
|
result.push_back(stoi(token));
|
|
}
|
|
|
|
return result;
|
|
}
|
|
|
|
string formatOutput(const vector<int> &output) {
|
|
if (output.empty())
|
|
return "[]";
|
|
|
|
stringstream ss;
|
|
ss << "[";
|
|
|
|
for (size_t i = 0; i < output.size(); ++i) {
|
|
ss << output[i];
|
|
if (i != output.size() - 1)
|
|
ss << ",";
|
|
}
|
|
|
|
ss << "]";
|
|
return ss.str();
|
|
}
|
|
|
|
int main() {
|
|
string line;
|
|
|
|
while (getline(cin, line)) {
|
|
vector<int> nums = parseIntArray(line);
|
|
|
|
getline(cin, line);
|
|
int target = stoi(line);
|
|
|
|
Solution sol;
|
|
vector<int> result = sol.twoSum(nums, target);
|
|
|
|
cout << formatOutput(result) << endl;
|
|
}
|
|
|
|
return 0;
|
|
}`,
|
|
},
|
|
],
|
|
},
|
|
testcases: {
|
|
create: [
|
|
{
|
|
data: {
|
|
create: [
|
|
{ label: "nums", value: "[2,7,11,15]", index: 0 },
|
|
{ label: "target", value: "9", index: 1 },
|
|
],
|
|
},
|
|
expectedOutput: "[0,1]",
|
|
},
|
|
{
|
|
data: {
|
|
create: [
|
|
{ label: "nums", value: "[3,2,4]", index: 0 },
|
|
{ label: "target", value: "6", index: 1 },
|
|
],
|
|
},
|
|
expectedOutput: "[1,2]",
|
|
},
|
|
{
|
|
data: {
|
|
create: [
|
|
{ label: "nums", value: "[3,3]", index: 0 },
|
|
{ label: "target", value: "6", index: 1 },
|
|
],
|
|
},
|
|
expectedOutput: "[0,1]",
|
|
},
|
|
],
|
|
},
|
|
},
|
|
{
|
|
displayId: 1001,
|
|
title: "Add Two Numbers",
|
|
description: `You are given two **non-empty** linked lists representing two non-negative integers. The digits are stored in **reverse order**, and each of their nodes contains a single digit. Add the two numbers and return the sum as a linked list.
|
|
|
|
You may assume the two numbers do not contain any leading zero, except the number 0 itself.
|
|
|
|
## Examples
|
|
|
|
### Example 1
|
|
|
|
|
|
|
|
\`\`\`shell
|
|
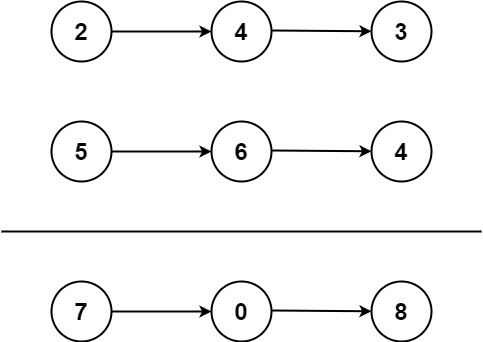
Input: l1 = [2,4,3], l2 = [5,6,4]
|
|
Output: [7,0,8]
|
|
Explanation: 342 + 465 = 807.
|
|
\`\`\`
|
|
|
|
### Example 2
|
|
|
|
\`\`\`shell
|
|
Input: l1 = [0], l2 = [0]
|
|
Output: [0]
|
|
\`\`\`
|
|
|
|
### Example 3
|
|
|
|
\`\`\`shell
|
|
Input: l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
|
|
Output: [8,9,9,9,0,0,0,1]
|
|
\`\`\`
|
|
|
|
## Constraints
|
|
|
|
<div align="center">
|
|
The number of nodes in each linked list is in the range $[1, 100]$.
|
|
</div>
|
|
|
|
\`\`\`math
|
|
0 <= Node.val <= 9
|
|
\`\`\`
|
|
|
|
<div align="center">
|
|
It is guaranteed that the list represents a number that does not have leading zeros.
|
|
</div>`,
|
|
solution: `## Approach 1: Elementary Math
|
|
|
|
### Intuition
|
|
|
|
Keep track of the carry using a variable and simulate digits-by-digits sum starting from the head of list, which contains the least-significant digit.
|
|
|
|

|
|
|
|
*Figure 1. Visualization of the addition of two numbers: $342 + 465 = 807$.*
|
|
|
|
*Each node contains a single digit and the digits are stored in reverse order.*
|
|
|
|
### Algorithm
|
|
|
|
Just like how you would sum two numbers on a piece of paper, we begin by summing the least-significant digits, which is the head of $l1$ and $l2$. Since each digit is in the range of $0…9$, summing two digits may "overflow". For example $5 + 7 = 12$. In this case, we set the current digit to $2$ and bring over the $carry = 1$ to the next iteration. $carry$ must be either $0$ or $1$ because the largest possible sum of two digits (including the carry) is $9 + 9 + 1 = 19$.
|
|
|
|
The pseudocode is as following:
|
|
|
|
- Initialize current node to dummy head of the returning list.
|
|
|
|
- Initialize carry to $0$.
|
|
|
|
- Loop through lists $l1$ and $l2$ until you reach both ends and carry is $0$.
|
|
|
|
- Set $x$ to node $l1$'s value. If $l1$ has reached the end of $l1$, set to $0$.
|
|
|
|
- Set $y$ to node $l2$'s value. If $l2$ has reached the end of $l2$, set to $0$.
|
|
|
|
- Set $sum = x + y + carry$.
|
|
|
|
- Update $carry = sum/10$.
|
|
|
|
- Create a new node with the digit value of ($sum$ $mod$ $10$) and set it to current node's next, then advance current node to next.
|
|
|
|
- Advance both $l1$ and $l2$.
|
|
|
|
- Return dummy head's next node.
|
|
|
|
Note that we use a dummy head to simplify the code. Without a dummy head, you would have to write extra conditional statements to initialize the head's value.
|
|
|
|
Take extra caution of the following cases:
|
|
|
|
| Test case | Explanation |
|
|
| ----------------------- | ----------------------------------------------------------------------------- |
|
|
| l1=[0,1]<br/>l2=[0,1,2] | When one list is longer than the other. |
|
|
| l1=[]<br/>l2=[0,1] | When one list is null, which means an empty list. |
|
|
| l1=[9,9]<br/>l2=[1] | The sum could have an extra carry of one at the end, which is easy to forget. |
|
|
|
|
### Implementation
|
|
|
|
\`\`\`c showLineNumbers
|
|
struct ListNode* addTwoNumbers(struct ListNode* l1, struct ListNode* l2) {
|
|
struct ListNode* dummyHead = malloc(sizeof(struct ListNode));
|
|
dummyHead->val = 0;
|
|
dummyHead->next = NULL;
|
|
struct ListNode* curr = dummyHead;
|
|
int carry = 0;
|
|
|
|
while (l1 != NULL || l2 != NULL || carry != 0) {
|
|
int x = (l1 != NULL) ? l1->val : 0;
|
|
int y = (l2 != NULL) ? l2->val : 0;
|
|
int sum = carry + x + y;
|
|
carry = sum / 10;
|
|
|
|
curr->next = malloc(sizeof(struct ListNode));
|
|
curr->next->val = sum % 10;
|
|
curr->next->next = NULL;
|
|
curr = curr->next;
|
|
|
|
if (l1 != NULL) l1 = l1->next;
|
|
if (l2 != NULL) l2 = l2->next;
|
|
}
|
|
|
|
struct ListNode* result = dummyHead->next;
|
|
free(dummyHead); // Free the memory allocated for dummyHead
|
|
return result;
|
|
}
|
|
\`\`\`
|
|
|
|
### Complexity Analysis
|
|
|
|
- **Time complexity:** $O(max(m,n))$
|
|
|
|
Assume that $m$ and $n$ represents the length of $l1$ and $l2$ respectively, the algorithm above iterates at most $max(m,n)$ times.
|
|
|
|
- **Space complexity:** $O(1)$
|
|
|
|
The length of the new list is at most $max(m,n) + 1$ However, we don't count the answer as part of the space complexity.
|
|
|
|
### Follow up
|
|
|
|
What if the the digits in the linked list are stored in non-reversed order? For example:
|
|
|
|
$(3 → 4 → 2) + (4 → 6 → 5) = 8 → 0 → 7$`,
|
|
difficulty: "MEDIUM",
|
|
published: true,
|
|
templates: {
|
|
create: [
|
|
{
|
|
language: "c",
|
|
template: `#include <stdio.h>
|
|
#include <stdlib.h>
|
|
#include <string.h>
|
|
|
|
struct ListNode {
|
|
int val;
|
|
struct ListNode *next;
|
|
};
|
|
|
|
struct ListNode *addTwoNumbers(struct ListNode *l1, struct ListNode *l2) {
|
|
|
|
}
|
|
|
|
struct ListNode *parseList(char *line) {
|
|
line[strcspn(line, "\\n")] = 0;
|
|
char *p = line;
|
|
while (*p && (*p == '[' || *p == ' ' || *p == ']'))
|
|
p++;
|
|
|
|
struct ListNode dummy;
|
|
struct ListNode *cur = &dummy;
|
|
dummy.next = NULL;
|
|
|
|
char *token = strtok(p, ",");
|
|
while (token) {
|
|
struct ListNode *node = malloc(sizeof(struct ListNode));
|
|
node->val = atoi(token);
|
|
node->next = NULL;
|
|
cur->next = node;
|
|
cur = node;
|
|
token = strtok(NULL, ",");
|
|
}
|
|
|
|
return dummy.next;
|
|
}
|
|
|
|
void printList(struct ListNode *head) {
|
|
printf("[");
|
|
while (head) {
|
|
printf("%d", head->val);
|
|
head = head->next;
|
|
if (head)
|
|
printf(",");
|
|
}
|
|
printf("]\\n");
|
|
}
|
|
|
|
void freeList(struct ListNode *head) {
|
|
while (head) {
|
|
struct ListNode *tmp = head;
|
|
head = head->next;
|
|
free(tmp);
|
|
}
|
|
}
|
|
|
|
int main() {
|
|
char line[1024];
|
|
while (fgets(line, sizeof(line), stdin)) {
|
|
struct ListNode *l1 = parseList(line);
|
|
if (!fgets(line, sizeof(line), stdin))
|
|
break;
|
|
struct ListNode *l2 = parseList(line);
|
|
|
|
struct ListNode *result = addTwoNumbers(l1, l2);
|
|
printList(result);
|
|
|
|
freeList(l1);
|
|
freeList(l2);
|
|
freeList(result);
|
|
}
|
|
return 0;
|
|
}`,
|
|
},
|
|
{
|
|
language: "cpp",
|
|
template: `#include <algorithm>
|
|
#include <iostream>
|
|
#include <sstream>
|
|
#include <string>
|
|
|
|
using namespace std;
|
|
|
|
struct ListNode {
|
|
int val;
|
|
ListNode *next;
|
|
ListNode() : val(0), next(nullptr) {}
|
|
ListNode(int x) : val(x), next(nullptr) {}
|
|
ListNode(int x, ListNode *next) : val(x), next(next) {}
|
|
};
|
|
|
|
class Solution {
|
|
public:
|
|
ListNode *addTwoNumbers(ListNode *l1, ListNode *l2) {
|
|
|
|
}
|
|
};
|
|
|
|
ListNode *createList(const string &line) {
|
|
ListNode dummy;
|
|
ListNode *tail = &dummy;
|
|
dummy.next = nullptr;
|
|
|
|
string nums = line;
|
|
nums.erase(remove(nums.begin(), nums.end(), '['), nums.end());
|
|
nums.erase(remove(nums.begin(), nums.end(), ']'), nums.end());
|
|
|
|
stringstream ss(nums);
|
|
string token;
|
|
while (getline(ss, token, ',')) {
|
|
if (!token.empty()) {
|
|
int val = stoi(token);
|
|
tail->next = new ListNode(val);
|
|
tail = tail->next;
|
|
}
|
|
}
|
|
|
|
return dummy.next;
|
|
}
|
|
|
|
void printList(ListNode *head) {
|
|
cout << "[";
|
|
while (head) {
|
|
cout << head->val;
|
|
if (head->next)
|
|
cout << ",";
|
|
head = head->next;
|
|
}
|
|
cout << "]" << endl;
|
|
}
|
|
|
|
void freeList(ListNode *head) {
|
|
while (head) {
|
|
ListNode *tmp = head;
|
|
head = head->next;
|
|
delete tmp;
|
|
}
|
|
}
|
|
|
|
int main() {
|
|
string line;
|
|
while (getline(cin, line)) {
|
|
ListNode *l1 = createList(line);
|
|
if (!getline(cin, line))
|
|
break;
|
|
ListNode *l2 = createList(line);
|
|
|
|
Solution sol;
|
|
ListNode *res = sol.addTwoNumbers(l1, l2);
|
|
printList(res);
|
|
|
|
freeList(l1);
|
|
freeList(l2);
|
|
freeList(res);
|
|
}
|
|
return 0;
|
|
}`,
|
|
},
|
|
],
|
|
},
|
|
testcases: {
|
|
create: [
|
|
{
|
|
data: {
|
|
create: [
|
|
{ label: "l1", value: "[2,4,3]", index: 0 },
|
|
{ label: "l2", value: "[5,6,4]", index: 1 },
|
|
],
|
|
},
|
|
expectedOutput: "[7,0,8]",
|
|
},
|
|
{
|
|
data: {
|
|
create: [
|
|
{ label: "l1", value: "[0]", index: 0 },
|
|
{ label: "l2", value: "[0]", index: 1 },
|
|
],
|
|
},
|
|
expectedOutput: "[0]",
|
|
},
|
|
{
|
|
data: {
|
|
create: [
|
|
{ label: "l1", value: "[9,9,9,9,9,9,9]", index: 0 },
|
|
{ label: "l2", value: "[9,9,9,9]", index: 1 },
|
|
],
|
|
},
|
|
expectedOutput: "[8,9,9,9,0,0,0,1]",
|
|
},
|
|
],
|
|
},
|
|
},
|
|
],
|
|
},
|
|
},
|
|
{
|
|
name: "fly6516",
|
|
email: "fly6516@outlook.com",
|
|
password: "$2b$10$SD1T/dYvKTArGdTmf8ERxuBKIONxY01/wSboRNaNsHnKZzDhps/0u",
|
|
role: "ADMIN",
|
|
problems: {
|
|
create: [
|
|
{
|
|
displayId: 1002,
|
|
title: "Median of Two Sorted Arrays",
|
|
description: `Given two sorted arrays \`nums1\` and \`nums2\` of size \`m\` and \`n\` respectively, return **the median** of the two sorted arrays.
|
|
|
|
The overall run time complexity should be $O(log(m+n))$.
|
|
|
|
## Examples
|
|
|
|
### Example 1
|
|
|
|
\`\`\`shell
|
|
Input: nums1 = [1,3], nums2 = [2]
|
|
Output: 2.00000
|
|
Explanation: merged array = [1,2,3] and median is 2.
|
|
\`\`\`
|
|
|
|
### Example 2
|
|
|
|
\`\`\`shell
|
|
Input: nums1 = [1,2], nums2 = [3,4]
|
|
Output: 2.50000
|
|
Explanation: merged array = [1,2,3,4] and median is (2 + 3) / 2 = 2.5.
|
|
\`\`\`
|
|
|
|
## Constraints
|
|
|
|
\`\`\`math
|
|
nums_1.length == m
|
|
\`\`\`
|
|
|
|
\`\`\`math
|
|
nums_2.length == n
|
|
\`\`\`
|
|
|
|
\`\`\`math
|
|
0 <= m <= 1000
|
|
\`\`\`
|
|
|
|
\`\`\`math
|
|
0 <= n <= 1000
|
|
\`\`\`
|
|
|
|
\`\`\`math
|
|
1 <= m + n <= 2000
|
|
\`\`\`
|
|
|
|
\`\`\`math
|
|
-10^6 <= nums_1[i], nums_2[i] <= 10^6
|
|
\`\`\``,
|
|
solution: `## Approach 1: Merge Sort
|
|
|
|
### Intuition
|
|
|
|
Let's start with the straightforward approach. If we put the elements of two arrays in one array \`A\` and arrange them in order. Assume the merged arrays has a length of \`n\`, then the median is:
|
|
|
|
- \`A[n / 2]\`, if \`n\` is odd.
|
|
|
|
- The average of \`A[n / 2]\` and \`A[n / 2 + 1]\`, if \`n\` is even.
|
|
|
|
However, we do not really need to merge and sort these arrays. Note that both arrays are already sorted, so the smallest element is either the first element of \`nums1\` or the first element of \`nums2\`. Therefore, we can set two pointers \`p1\` and \`p2\` at the start of each array, then we can get the smallest element from the \`nums1\` and \`nums2\` by comparing the values \`nums1[p1]\` and \`nums2[p2]\`.
|
|
|
|
Please refer to the following slide as an example:
|
|
|
|
### Algorithm
|
|
|
|
1. Get the total size of two arrays \`m + n\`
|
|
|
|
- If \`m + n\` is odd, we are looking for the \`(m + n) / 2\` -th element.
|
|
|
|
- If \`m + n\` is even, we are looking for the average of the \`(m + n) / 2\` -th and the \`(m + n) / 2 + 1\` -th elements.
|
|
|
|
2. Set two pointers \`p1\` and \`p2\` at the beginning of arrays \`nums1\` and \`nums2\`.
|
|
|
|
3. If both \`p1\` and \`p2\` are in bounds of the arrays, compare the values at \`p1\` and \`p2\`:
|
|
|
|
- If \`nums1[p1]\` is smaller than \`nums2[p2]\`, we move \`p1\` one place to the right.
|
|
|
|
- Otherwise, we move \`p2\` one place to the right.
|
|
|
|
If \`p1\` is outside \`nums1\`, just move \`p2\` one place to the right.
|
|
|
|
If \`p2\` is outside \`nums2\`, just move \`p1\` one place to the right.
|
|
|
|
4. Get the target elements and calculate the median:
|
|
|
|
- If \`m + n\` is odd, repeat step 3 by \`(m + n + 1) / 2\` times and return the element from the last step.
|
|
|
|
- If \`m + n\` is even, repeat step 3 by \`(m + n) / 2 + 1\` times and return the average of the elements from the last two steps.
|
|
|
|
### Implementation
|
|
|
|
\`\`\`c showLineNumbers
|
|
double findMedianSortedArrays(int* nums1, int nums1Size, int* nums2, int nums2Size) {
|
|
int m = nums1Size, n = nums2Size;
|
|
int p1 = 0, p2 = 0;
|
|
|
|
int getMin() {
|
|
if (p1 < m && p2 < n) {
|
|
return nums1[p1] < nums2[p2] ? nums1[p1++] : nums2[p2++];
|
|
} else if (p1 < m) {
|
|
return nums1[p1++];
|
|
} else if (p2 < n) {
|
|
return nums2[p2++];
|
|
}
|
|
return -1;
|
|
}
|
|
|
|
double median;
|
|
if ((m + n) % 2 == 0) {
|
|
for (int i = 0; i < ((m + n) / 2) - 1; ++i) {
|
|
int temp = getMin();
|
|
}
|
|
median = (getMin() + getMin()) / 2.0;
|
|
} else {
|
|
for (int i = 0; i < (m + n) / 2; ++i) {
|
|
int temp = getMin();
|
|
}
|
|
median = getMin();
|
|
}
|
|
|
|
return median;
|
|
}
|
|
\`\`\`
|
|
|
|
### Complexity Analysis
|
|
|
|
Let $m$ be the size of array \`nums1\` and $n$ be the size of array \`nums2\`.
|
|
|
|
- **Time complexity:** $O(m + n)$
|
|
|
|
- We get the smallest element by comparing two values at \`p1\` and \`p2\`, it takes $O(1)$ to compare two elements and move the corresponding pointer to the right.
|
|
|
|
- We need to traverse half of the arrays before reaching the median element(s).
|
|
|
|
- To sum up, the time complexity is $O(m + n)$.
|
|
|
|
- **Space complexity:** $O(1)$
|
|
|
|
- We only need to maintain two pointers \`p1\` and \`p2\`.`,
|
|
difficulty: "HARD",
|
|
published: true,
|
|
templates: {
|
|
create: [
|
|
{
|
|
language: "c",
|
|
template: `#include <stdio.h>
|
|
#include <stdlib.h>
|
|
#include <string.h>
|
|
|
|
double findMedianSortedArrays(int* nums1, int nums1Size, int* nums2, int nums2Size) {
|
|
|
|
}
|
|
|
|
int *parseIntArray(char *line, int *len) {
|
|
line[strcspn(line, "\\n")] = 0;
|
|
char *p = line;
|
|
while (*p && (*p == '[' || *p == ' ' || *p == ']'))
|
|
p++;
|
|
|
|
int capacity = 10;
|
|
int *arr = malloc(capacity * sizeof(int));
|
|
*len = 0;
|
|
|
|
char *token = strtok(p, ",");
|
|
while (token) {
|
|
if (*len >= capacity) {
|
|
capacity *= 2;
|
|
arr = realloc(arr, capacity * sizeof(int));
|
|
}
|
|
arr[(*len)++] = atoi(token);
|
|
token = strtok(NULL, ",");
|
|
}
|
|
return arr;
|
|
}
|
|
|
|
int main() {
|
|
char line[1024];
|
|
|
|
while (fgets(line, sizeof(line), stdin)) {
|
|
int nums1Size;
|
|
int *nums1 = parseIntArray(line, &nums1Size);
|
|
|
|
if (!fgets(line, sizeof(line), stdin))
|
|
break;
|
|
int nums2Size;
|
|
int *nums2 = parseIntArray(line, &nums2Size);
|
|
|
|
double result = findMedianSortedArrays(nums1, nums1Size, nums2, nums2Size);
|
|
printf("%.5f\\n", result);
|
|
|
|
free(nums1);
|
|
free(nums2);
|
|
}
|
|
|
|
return 0;
|
|
}`,
|
|
},
|
|
{
|
|
language: "cpp",
|
|
template: `#include <iostream>
|
|
#include <sstream>
|
|
#include <string>
|
|
#include <vector>
|
|
|
|
using namespace std;
|
|
|
|
class Solution {
|
|
public:
|
|
double findMedianSortedArrays(vector<int> &nums1, vector<int> &nums2) {
|
|
|
|
}
|
|
};
|
|
|
|
vector<int> parseVector(const string &line) {
|
|
vector<int> result;
|
|
stringstream ss(line);
|
|
char c;
|
|
int num;
|
|
while (ss >> c) {
|
|
if (isdigit(c) || c == '-' || c == '+') {
|
|
ss.putback(c);
|
|
ss >> num;
|
|
result.push_back(num);
|
|
}
|
|
}
|
|
return result;
|
|
}
|
|
|
|
int main() {
|
|
string line;
|
|
while (getline(cin, line)) {
|
|
vector<int> nums1 = parseVector(line);
|
|
|
|
if (!getline(cin, line))
|
|
break;
|
|
vector<int> nums2 = parseVector(line);
|
|
|
|
Solution sol;
|
|
double result = sol.findMedianSortedArrays(nums1, nums2);
|
|
printf("%.5f\\n", result);
|
|
}
|
|
return 0;
|
|
}`,
|
|
},
|
|
],
|
|
},
|
|
testcases: {
|
|
create: [
|
|
{
|
|
data: {
|
|
create: [
|
|
{ label: "nums1", value: "[1,3]", index: 0 },
|
|
{ label: "nums2", value: "[2]", index: 1 },
|
|
],
|
|
},
|
|
expectedOutput: "2.00000",
|
|
},
|
|
{
|
|
data: {
|
|
create: [
|
|
{ label: "nums1", value: "[1,2]", index: 0 },
|
|
{ label: "nums2", value: "[3,4]", index: 1 },
|
|
],
|
|
},
|
|
expectedOutput: "2.50000",
|
|
},
|
|
],
|
|
},
|
|
},
|
|
],
|
|
},
|
|
},
|
|
];
|
|
|
|
export async function main() {
|
|
for (const e of editorLanguageConfigData) {
|
|
await prisma.editorLanguageConfig.create({ data: e });
|
|
}
|
|
|
|
for (const u of userData) {
|
|
await prisma.user.create({ data: u });
|
|
}
|
|
}
|
|
|
|
main();
|