diff --git a/prisma/seed-cn.ts b/prisma/seed-cn.ts
new file mode 100644
index 0000000..5d64961
--- /dev/null
+++ b/prisma/seed-cn.ts
@@ -0,0 +1,1105 @@
+import { PrismaClient, Prisma, EditorLanguage, LanguageServerProtocol } from "@/generated/client";
+
+const prisma = new PrismaClient();
+
+const editorLanguageConfigData: Prisma.EditorLanguageConfigCreateInput[] = [
+    {
+        language: EditorLanguage.c,
+        label: "C",
+        fileName: "main",
+        fileExtension: ".c",
+        languageServerConfig: {
+            create: {
+                protocol: LanguageServerProtocol.ws,
+                hostname: "localhost",
+                port: 4594,
+                path: "/clangd",
+            },
+        },
+        dockerConfig: {
+            create: {
+                image: "gcc",
+                tag: "latest",
+                workingDir: "/src",
+                compileOutputLimit: 1 * 1024 * 1024,
+                runOutputLimit: 1 * 1024 * 1024,
+            },
+        },
+    },
+    {
+        language: EditorLanguage.cpp,
+        label: "C++",
+        fileName: "main",
+        fileExtension: ".cpp",
+        languageServerConfig: {
+            create: {
+                protocol: LanguageServerProtocol.ws,
+                hostname: "localhost",
+                port: 4595,
+                path: "/clangd",
+            },
+        },
+        dockerConfig: {
+            create: {
+                image: "gcc",
+                tag: "latest",
+                workingDir: "/src",
+                compileOutputLimit: 1 * 1024 * 1024,
+                runOutputLimit: 1 * 1024 * 1024,
+            },
+        },
+    },
+];
+
+const userData: Prisma.UserCreateInput[] = [
+    {
+        name: "cfngc4594",
+        email: "cfngc4594@gmail.com",
+        password: "$2b$10$edWXpq2TOiiGQkPOXWKGlO4EKnp2YyV7OoS2qqk/W0E6GyiVQIC66",
+        role: "ADMIN",
+        problems: {
+            create: [
+                {
+                    displayId: 1000,
+                    title: "两数之和",
+                    description: `#### 1. 两数之和
+
+难度：简单
+
+---
+
+给定一个整数数组 \`nums\` 和一个整数目标值 \`target\`，请你在该数组中找出  **和为目标值**  _\`target\`_  的那  **两个**  整数，并返回它们的数组下标。
+
+你可以假设每种输入只会对应一个答案，并且你不能使用两次相同的元素。
+
+你可以按任意顺序返回答案。
+
+ **示例 1：** 
+
+\`\`\`
+输入：nums = [2,7,11,15], target = 9
+输出：[0,1]
+解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。
+\`\`\`
+
+ **示例 2：** 
+
+\`\`\`
+输入：nums = [3,2,4], target = 6
+输出：[1,2]
+\`\`\`
+
+ **示例 3：** 
+
+\`\`\`
+输入：nums = [3,3], target = 6
+输出：[0,1]
+\`\`\`
+
+ **提示：** 
+
+*   \`2 <= nums.length <= 10^4\`
+*   \`-10^9 <= nums[i] <= 10^9\`
+*   \`-10^9 <= target <= 10^9\`
+*    **只会存在一个有效答案** 
+
+ **进阶：** 你可以想出一个时间复杂度小于 \`O(n^2)\` 的算法吗？
+
+---
+
+
+
+\`\`\`C++
+\`\`\``,
+                    solution: `<VideoEmbed platform="youtube" id="tSI98g3PDyE" />
+
+## 方法一：暴力枚举
+
+### 思路及算法
+
+最容易想到的方法是枚举数组中的每一个数 x，寻找数组中是否存在 target - x。
+
+当我们使用遍历整个数组的方式寻找 target - x 时，需要注意到每一个位于 x 之前的元素都已经和 x 匹配过，因此不需要再进行匹配。而每一个元素不能被使用两次，所以我们只需要在 x 后面的元素中寻找 target - x。
+
+
+### 代码
+
+\`\`\`c showLineNumbers
+int* twoSum(int* nums, int numsSize, int target, int* returnSize) {
+    struct hashTable {
+        int key;
+        int value;
+        UT_hash_handle hh;
+    } *hashTable = NULL, *item, *tmpItem;
+
+    for (int i = 0; i < numsSize; i++) {
+        HASH_FIND_INT(hashTable, &nums[i], item);
+        if (item) {
+            int* result = malloc(sizeof(int) * 2);
+            result[0] = item->value;
+            result[1] = i;
+            *returnSize = 2;
+            HASH_ITER(hh, hashTable, item, tmpItem) {
+                HASH_DEL(hashTable, item);
+                free(item);
+            }
+            return result;
+        }
+        item = malloc(sizeof(struct hashTable));
+        item->key = target - nums[i];
+        item->value = i;
+        HASH_ADD_INT(hashTable, key, item);
+    }
+
+    HASH_ITER(hh, hashTable, item, tmpItem) {
+        HASH_DEL(hashTable, item);
+        free(item);
+    }
+
+    *returnSize = 0;
+    // If no valid pair is found, return an empty array
+    return malloc(sizeof(int) * 0);
+}
+
+\`\`\`
+
+### 复杂度分析
+
+- **时间复杂度:** $O(n^2)$.
+
+  其中 $n$ 是数组中的元素数量。最坏情况下数组中任意两个数都要被匹配一次。
+
+- **空间复杂度:** $O(1)$.
+
+  所需的空间不取决于 input 数组的大小，因此仅使用恒定空间。
+
+---
+
+## 方法二：哈希表
+
+### 思路及算法
+
+注意到方法一的时间复杂度较高的原因是寻找 target - x 的时间复杂度过高。因此，我们需要一种更优秀的方法，能够快速寻找数组中是否存在目标元素。如果存在，我们需要找出它的索引。
+
+使用哈希表，可以将寻找 target - x 的时间复杂度降低到从 $O(N)$ 降低到 $O(1)$。
+
+这样我们创建一个哈希表，对于每一个 x，我们首先查询哈希表中是否存在 target - x，然后将 x 插入到哈希表中，即可保证不会让 x 和自己匹配。
+
+### 代码
+
+\`\`\`c showLineNumbers
+int* twoSum(int* nums, int numsSize, int target, int* returnSize) {
+    struct hashTable {
+        int key;
+        int value;
+        UT_hash_handle hh;
+    } *hashTable = NULL, *item, *tmpItem;
+
+    for (int i = 0; i < numsSize; i++) {
+        HASH_FIND_INT(hashTable, &nums[i], item);
+        if (item) {
+            int* result = malloc(sizeof(int) * 2);
+            result[0] = item->value;
+            result[1] = i;
+            *returnSize = 2;
+            HASH_ITER(hh, hashTable, item, tmpItem) {
+                HASH_DEL(hashTable, item);
+                free(item);
+            }
+            return result;
+        }
+        item = malloc(sizeof(struct hashTable));
+        item->key = target - nums[i];
+        item->value = i;
+        HASH_ADD_INT(hashTable, key, item);
+    }
+
+    HASH_ITER(hh, hashTable, item, tmpItem) {
+        HASH_DEL(hashTable, item);
+        free(item);
+    }
+
+    *returnSize = 0;
+    // If no valid pair is found, return an empty array
+    return malloc(sizeof(int) * 0);
+}
+\`\`\`
+
+### 复杂度分析
+
+- **时间复杂度:** $O(n)$.
+
+  其中 $N$ 是数组中的元素数量。对于每一个元素 x，我们可以 $O(1)$ 地寻找 target - x。
+  
+- **空间复杂度:** $O(n)$.
+
+  其中 $N$ 是数组中的元素数量。主要为哈希表的开销。
+`,
+                    difficulty: "EASY",
+                    published: true,
+                    templates: {
+                        create: [
+                            {
+                                language: "c",
+                                template: `
+#include <stdio.h>
+#include <stdlib.h>
+#include <string.h>
+
+int *parseIntArray(char *line, int *len) {
+  line[strcspn(line, "\\n")] = 0;
+  char *p = line;
+  while (*p && (*p == '[' || *p == ' ' || *p == ']'))
+    p++;
+
+  int capacity = 10;
+  int *arr = malloc(capacity * sizeof(int));
+  *len = 0;
+
+  char *token = strtok(p, ",");
+  while (token) {
+    if (*len >= capacity) {
+      capacity *= 2;
+      arr = realloc(arr, capacity * sizeof(int));
+    }
+    arr[(*len)++] = atoi(token);
+    token = strtok(NULL, ",");
+  }
+  return arr;
+}
+
+char *formatOutput(int *res, int resLen) {
+  if (resLen == 0)
+    return "[]";
+
+  char *buf = malloc(resLen * 12 + 3);
+  char *p = buf;
+  *p++ = '[';
+  for (int i = 0; i < resLen; i++) {
+    p += sprintf(p, "%d", res[i]);
+    if (i != resLen - 1)
+      *p++ = ',';
+  }
+  *p++ = ']';
+  *p = 0;
+  return buf;
+}
+
+int *twoSum(int *nums, int numsSize, int target, int *returnSize);
+
+int main() {
+  char line[1024];
+  while (fgets(line, sizeof(line), stdin)) {
+    int numsSize;
+    int *nums = parseIntArray(line, &numsSize);
+
+    if (!fgets(line, sizeof(line), stdin))
+      break;
+    int target = atoi(line);
+
+    int returnSize;
+    int *res = twoSum(nums, numsSize, target, &returnSize);
+
+    char *output = formatOutput(res, returnSize);
+    printf("%s\\n", output);
+
+    free(nums);
+    if (returnSize > 0)
+      free(res);
+    if (returnSize > 0)
+      free(output);
+  }
+  return 0;
+}
+
+/**
+ * Note: The returned array must be malloced, assume caller calls free().
+ */
+int* twoSum(int* nums, int numsSize, int target, int* returnSize) {
+    
+}`,
+                            },
+                            {
+                                language: "cpp",
+                                template: `
+#include <iostream>
+#include <vector>
+#include <string>
+#include <sstream>
+#include <algorithm>
+#include <unordered_map>
+
+using namespace std;
+
+// 解析输入字符串为整数数组
+vector<int> parseIntArray(string line) {
+    vector<int> result;
+    line.erase(remove(line.begin(), line.end(), '['), line.end());
+    line.erase(remove(line.begin(), line.end(), ']'), line.end());
+    stringstream ss(line);
+    string token;
+    while (getline(ss, token, ',')) {
+        if (!token.empty()) {
+            result.push_back(stoi(token));
+        }
+    }
+    return result;
+}
+
+// 格式化输出结果为字符串
+string formatOutput(const vector<int>& res) {
+    if (res.empty()) return "[]";
+    stringstream ss;
+    ss << "[";
+    for (size_t i = 0; i < res.size(); ++i) {
+        ss << res[i];
+        if (i != res.size() - 1)
+            ss << ",";
+    }
+    ss << "]";
+    return ss.str();
+}
+
+// Solution 类声明
+class Solution {
+public:
+    vector<int> twoSum(vector<int>& nums, int target);
+};
+
+int main() {
+    string line;
+    while (getline(cin, line)) {
+        vector<int> nums = parseIntArray(line);
+
+        if (!getline(cin, line)) break;
+        int target = stoi(line);
+
+        Solution sol;
+        vector<int> res = sol.twoSum(nums, target);
+
+        cout << formatOutput(res) << endl;
+    }
+
+    return 0;
+}
+
+vector<int> Solution::twoSum(vector<int>& nums, int target) {
+
+    return {};
+}
+`,
+                            },
+                        ],
+                    },
+                    testcases: {
+                        create: [
+                            {
+                                data: {
+                                    create: [
+                                        { label: "nums", value: "[2,7,11,15]", index: 0 },
+                                        { label: "target", value: "9", index: 1 },
+                                    ],
+                                },
+                                expectedOutput: "[0,1]",
+                            },
+                            {
+                                data: {
+                                    create: [
+                                        { label: "nums", value: "[3,2,4]", index: 0 },
+                                        { label: "target", value: "6", index: 1 },
+                                    ],
+                                },
+                                expectedOutput: "[1,2]",
+                            },
+                            {
+                                data: {
+                                    create: [
+                                        { label: "nums", value: "[3,3]", index: 0 },
+                                        { label: "target", value: "6", index: 1 },
+                                    ],
+                                },
+                                expectedOutput: "[0,1]",
+                            },
+                        ],
+                    },
+                },
+                {
+                    displayId: 1001,
+                    title: "两数相加",
+                    description: `#### 2. 两数相加
+
+难度：中等
+
+---
+
+给你两个  **非空**  的链表，表示两个非负的整数。它们每位数字都是按照  **逆序**  的方式存储的，并且每个节点只能存储  **一位**  数字。
+
+请你将两个数相加，并以相同形式返回一个表示和的链表。
+
+你可以假设除了数字 0 之外，这两个数都不会以 0 开头。
+
+ **示例 1：** 
+
+![](https://assets.leetcode-cn.com/aliyun-lc-upload/uploads/2021/01/02/addtwonumber1.jpg)
+\`\`\`
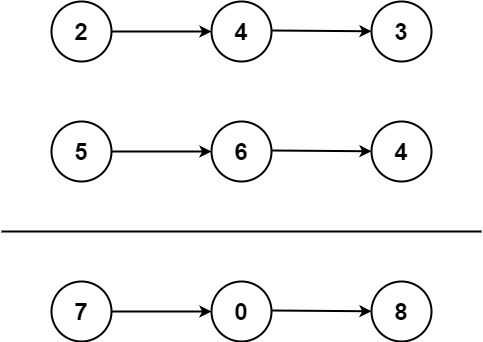
+输入：l1 = [2,4,3], l2 = [5,6,4]
+输出：[7,0,8]
+解释：342 + 465 = 807.
+\`\`\`
+
+ **示例 2：** 
+
+\`\`\`
+输入：l1 = [0], l2 = [0]
+输出：[0]
+\`\`\`
+
+ **示例 3：** 
+
+\`\`\`
+输入：l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
+输出：[8,9,9,9,0,0,0,1]
+\`\`\`
+
+ **提示：** 
+
+*   每个链表中的节点数在范围 \`[1, 100]\` 内
+*   \`0 <= Node.val <= 9\`
+*   题目数据保证列表表示的数字不含前导零
+
+---
+
+
+
+\`\`\`C++
+\`\`\``,
+                    solution: `## 方法一：模拟
+
+### 思路与算法
+
+由于输入的两个链表都是逆序存储数字的位数的，因此两个链表中同一位置的数字可以直接相加。
+
+我们同时遍历两个链表，逐位计算它们的和，并与当前位置的进位值相加。具体而言，如果当前两个链表处相应位置的数字为 n1,n2，进位值为 carry，则它们的和为 n1+n2+carry；其中，答案链表处相应位置的数字为 (n1+n2+carry)mod10，而新的进位值为 ⌊ 
+10
+
+
+如果两个链表的长度不同，则可以认为长度短的链表的后面有若干个 0 。
+
+此外，如果链表遍历结束后，有 carry>0，还需要在答案链表的后面附加一个节点，节点的值为 carry。
+
+
+
+### 代码
+
+\`\`\`c showLineNumbers
+struct ListNode* addTwoNumbers(struct ListNode* l1, struct ListNode* l2) {
+    struct ListNode* dummyHead = malloc(sizeof(struct ListNode));
+    dummyHead->val = 0;
+    dummyHead->next = NULL;
+    struct ListNode* curr = dummyHead;
+    int carry = 0;
+
+    while (l1 != NULL || l2 != NULL || carry != 0) {
+        int x = (l1 != NULL) ? l1->val : 0;
+        int y = (l2 != NULL) ? l2->val : 0;
+        int sum = carry + x + y;
+        carry = sum / 10;
+
+        curr->next = malloc(sizeof(struct ListNode));
+        curr->next->val = sum % 10;
+        curr->next->next = NULL;
+        curr = curr->next;
+
+        if (l1 != NULL) l1 = l1->next;
+        if (l2 != NULL) l2 = l2->next;
+    }
+
+    struct ListNode* result = dummyHead->next;
+    free(dummyHead);  // Free the memory allocated for dummyHead
+    return result;
+}
+\`\`\`
+
+### 复杂度分析
+
+- **时间复杂度:** $O(max(m,n))$
+
+  其中 $m$ 和 $n$ 分别为两个链表的长度。我们要遍历两个链表的全部位置，而处理每个位置只需要 $O(1)$ 的时间。
+  
+- **空间复杂度:** $O(1)$
+
+  注意返回值不计入空间复杂度。
+  
+`,
+                    difficulty: "MEDIUM",
+                    published: true,
+                    templates: {
+                        create: [
+                            {
+                                language: "c",
+                                template: `
+#include <stdio.h>
+#include <stdlib.h>
+#include <string.h>
+
+// Definition for singly-linked list.
+struct ListNode {
+    int val;
+    struct ListNode *next;
+};
+
+// 创建链表
+struct ListNode* createList(char *line) {
+    struct ListNode dummy;
+    struct ListNode *tail = &dummy;
+    dummy.next = NULL;
+
+    line[strcspn(line, "\\n")] = 0;
+    char *p = line;
+    while (*p && (*p == '[' || *p == ' ' || *p == ']')) p++;
+
+    char *token = strtok(p, ",");
+    while (token) {
+        struct ListNode *node = malloc(sizeof(struct ListNode));
+        node->val = atoi(token);
+        node->next = NULL;
+        tail->next = node;
+        tail = node;
+        token = strtok(NULL, ",");
+    }
+
+    return dummy.next;
+}
+
+// 打印链表
+void printList(struct ListNode* head) {
+    printf("[");
+    while (head) {
+        printf("%d", head->val);
+        if (head->next) printf(",");
+        head = head->next;
+    }
+    printf("]\\n");
+}
+
+// 释放链表内存
+void freeList(struct ListNode* head) {
+    while (head) {
+        struct ListNode* temp = head;
+        head = head->next;
+        free(temp);
+    }
+}
+
+// 主函数
+int main() {
+    char line[1024];
+
+    while (fgets(line, sizeof(line), stdin)) {
+        struct ListNode* l1 = createList(line);
+
+        if (!fgets(line, sizeof(line), stdin)) break;
+        struct ListNode* l2 = createList(line);
+
+        struct ListNode* result = addTwoNumbers(l1, l2);
+        printList(result);
+
+        freeList(l1);
+        freeList(l2);
+        freeList(result);
+    }
+
+    return 0;
+}
+
+
+struct ListNode* addTwoNumbers(struct ListNode* l1, struct ListNode* l2) {
+    
+    return NULL; // 在这里填充你的算法逻辑
+}
+
+`,
+                            },
+                            {
+                                language: "cpp",
+                                template: `
+#include <iostream>
+#include <string>
+#include <sstream>
+#include <vector>
+#include <algorithm>
+using namespace std;
+
+// Definition for singly-linked list.
+struct ListNode {
+    int val;
+    ListNode *next;
+    ListNode() : val(0), next(nullptr) {}
+    ListNode(int x) : val(x), next(nullptr) {}
+    ListNode(int x, ListNode *next) : val(x), next(next) {}
+};
+
+// 声明 Solution 类
+class Solution {
+public:
+    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2);
+};
+
+// 输入字符串 -> 链表
+ListNode* createList(const string& line) {
+    ListNode dummy;
+    ListNode* tail = &dummy;
+    dummy.next = nullptr;
+
+    string nums = line;
+    nums.erase(remove(nums.begin(), nums.end(), '['), nums.end());
+    nums.erase(remove(nums.begin(), nums.end(), ']'), nums.end());
+
+    stringstream ss(nums);
+    string token;
+    while (getline(ss, token, ',')) {
+        if (!token.empty()) {
+            int val = stoi(token);
+            tail->next = new ListNode(val);
+            tail = tail->next;
+        }
+    }
+
+    return dummy.next;
+}
+
+// 打印链表
+void printList(ListNode* head) {
+    cout << "[";
+    while (head) {
+        cout << head->val;
+        if (head->next) cout << ",";
+        head = head->next;
+    }
+    cout << "]" << endl;
+}
+
+// 释放内存
+void freeList(ListNode* head) {
+    while (head) {
+        ListNode* tmp = head;
+        head = head->next;
+        delete tmp;
+    }
+}
+
+// 主函数
+int main() {
+    string line;
+    while (getline(cin, line)) {
+        ListNode* l1 = createList(line);
+        if (!getline(cin, line)) break;
+        ListNode* l2 = createList(line);
+
+        Solution sol;
+        ListNode* res = sol.addTwoNumbers(l1, l2);
+        printList(res);
+
+        freeList(l1);
+        freeList(l2);
+        freeList(res);
+    }
+    return 0;
+}
+
+
+ListNode* Solution::addTwoNumbers(ListNode* l1, ListNode* l2) {
+
+    return nullptr; // 在这里填充你的算法逻辑
+}
+`,
+                            },
+                        ],
+                    },
+                    testcases: {
+                        create: [
+                            {
+                                data: {
+                                    create: [
+                                        { label: "l1", value: "[2,4,3]", index: 0 },
+                                        { label: "l2", value: "[5,6,4]", index: 1 },
+                                    ],
+                                },
+                                expectedOutput: "[7,0,8]",
+                            },
+                            {
+                                data: {
+                                    create: [
+                                        { label: "l1", value: "[0]", index: 0 },
+                                        { label: "l2", value: "[0]", index: 1 },
+                                    ],
+                                },
+                                expectedOutput: "[0]",
+                            },
+                            {
+                                data: {
+                                    create: [
+                                        { label: "l1", value: "[9,9,9,9,9,9,9]", index: 0 },
+                                        { label: "l2", value: "[9,9,9,9]", index: 1 },
+                                    ],
+                                },
+                                expectedOutput: "[8,9,9,9,0,0,0,1]",
+                            },
+                        ],
+                    },
+                },
+            ],
+        },
+    },
+    {
+        name: "fly6516",
+        email: "fly6516@outlook.com",
+        password: "$2b$10$SD1T/dYvKTArGdTmf8ERxuBKIONxY01/wSboRNaNsHnKZzDhps/0u",
+        role: "ADMIN",
+        problems: {
+            create: [
+                {
+                    displayId: 1002,
+                    title: "寻找两个正序数组的中位数",
+                    description: `#### 4. 寻找两个正序数组的中位数
+
+难度：困难
+
+---
+
+给定两个大小分别为 \`m\` 和 \`n\` 的正序（从小到大）数组 \`nums1\` 和 \`nums2\`。请你找出并返回这两个正序数组的  **中位数**  。
+
+算法的时间复杂度应该为 \`O(log (m+n))\` 。
+
+ **示例 1：** 
+
+\`\`\`
+输入：nums1 = [1,3], nums2 = [2]
+输出：2.00000
+解释：合并数组 = [1,2,3] ，中位数 2
+\`\`\`
+
+ **示例 2：** 
+
+\`\`\`
+输入：nums1 = [1,2], nums2 = [3,4]
+输出：2.50000
+解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5
+\`\`\`
+
+ **提示：** 
+
+*   \`nums1.length == m\`
+*   \`nums2.length == n\`
+*   \`0 <= m <= 1000\`
+*   \`0 <= n <= 1000\`
+*   \`1 <= m + n <= 2000\`
+*   \`-10^6 <= nums1[i], nums2[i] <= 10^6\`
+
+---
+
+
+
+\`\`\`C++
+\`\`\``,
+                    solution: `## 方法一：二分查找
+
+### Intuition
+
+给定两个有序数组，要求找到两个有序数组的中位数，最直观的思路有以下两种：
+
+- 使用归并的方式，合并两个有序数组，得到一个大的有序数组。大的有序数组的中间位置的元素，即为中位数。
+
+- 不需要合并两个有序数组，只要找到中位数的位置即可。由于两个数组的长度已知，因此中位数对应的两个数组的下标之和也是已知的。维护两个指针，初始时分别指向两个数组的下标 0 的位置，每次将指向较小值的指针后移一位（如果一个指针已经到达数组末尾，则只需要移动另一个数组的指针），直到到达中位数的位置。
+
+
+#假设两个有序数组的长度分别为 $m$ 和 $n$，上述两种思路的复杂度如何？
+
+第一种思路的时间复杂度是 $O(m+n)$，空间复杂度是 $O(m+n)$。第二种思路虽然可以将空间复杂度降到 $O(1)$，但是时间复杂度仍是 $O(m+n)$。
+
+如何把时间复杂度降低到 $O(log(m+n))$ 呢？如果对时间复杂度的要求有 $log$，通常都需要用到二分查找，这道题也可以通过二分查找实现。
+
+根据中位数的定义，当 $m+n$ 是奇数时，中位数是两个有序数组中的第 $(m+n)/2$ 个元素，当 $m+n$ 是偶数时，中位数是两个有序数组中的第 $(m+n)/2$ 个元素和第 $(m+n)/2+1$ 个元素的平均值。因此，这道题可以转化成寻找两个有序数组中的第 $k$ 小的数，其中 $k$ 为 $(m+n)/2$ 或 $(m+n)/2+1$。
+
+假设两个有序数组分别是 $A$ 和 $B$。要找到第 $k$ 个元素，我们可以比较 $A[k/2−1]$ 和 $B[k/2−1]$，其中 $/$ 表示整数除法。由于 $A[k/2−1]$ 和 $B[k/2−1]$ 的前面分别有 $A[0..k/2−2]$ 和 $B[0..k/2−2]$，即 $k/2−1$ 个元素，对于 $A[k/2−1]$ 和 $B[k/2−1]$ 中的较小值，最多只会有 $(k/2−1)+(k/2−1)≤k−2$ 个元素比它小，那么它就不能是第 $k$ 小的数了。
+
+
+ ![](https://assets.leetcode-cn.com/solution-static/4/4_fig1.png）
+ 
+ 因此我们可以归纳出三种情况：
+
+- 如果 $A[k/2−1]<B[k/2−1]$，则比 $A[k/2−1]$ 小的数最多只有 $A$ 的前 $k/2−1$ 个数和 $B$ 的前 $k/2−1$ 个数，即比 $A[k/2−1]$ 小的数最多只有 $k−2$ 个，因此 $A[k/2−1]$ 不可能是第 $k$ 个数，$A[0]$ 到 $A[k/2−1]$ 也都不可能是第 $k$ 个数，可以全部排除。
+
+- 如果 $A[k/2−1]>B[k/2−1]$，则可以排除 $B[0]$ 到 $B[k/2−1]$。
+
+- 如果 $A[k/2−1]=B[k/2−1]$，则可以归入第一种情况处理。
+
+可以看到，比较 $A[k/2−1] 和 $B[k/2−1]$ 之后，可以排除 $k/2$ 个不可能是第 $k$ 小的数，查找范围缩小了一半。同时，我们将在排除后的新数组上继续进行二分查找，并且根据我们排除数的个数，减少 $k$ 的值，这是因为我们排除的数都不大于第 $k$ 小的数。
+
+有以下三种情况需要特殊处理：
+
+- 如果 $A[k/2−1]$ 或者 $B[k/2−1]$ 越界，那么我们可以选取对应数组中的最后一个元素。在这种情况下，我们必须根据排除数的个数减少 $k$ 的值，而不能直接将 $k$ 减去 $k/2$。
+
+- 如果一个数组为空，说明该数组中的所有元素都被排除，我们可以直接返回另一个数组中第 $k$ 小的元素。
+
+- 如果 $k=1$，我们只要返回两个数组首元素的最小值即可。
+
+用一个例子说明上述算法。假设两个有序数组如下：
+\`\`\`math
+A: 1 3 4 9
+B: 1 2 3 4 5 6 7 8 9
+\`\`\`
+
+两个有序数组的长度分别是 4 和 9，长度之和是 13，中位数是两个有序数组中的第 7 个元素，因此需要找到第 k=7 个元素。
+
+比较两个有序数组中下标为 k/2−1=2 的数，即 A[2] 和 B[2]，如下面所示：
+\`\`\`math
+A: 1 3 4 9
+       ↑
+B: 1 2 3 4 5 6 7 8 9
+       ↑
+\`\`\`
+由于 A[2]>B[2]，因此排除 B[0] 到 B[2]，即数组 B 的下标偏移（offset）变为 3，同时更新 k 的值：k=k−k/2=4。
+
+下一步寻找，比较两个有序数组中下标为 k/2−1=1 的数，即 A[1] 和 B[4]，如下面所示，其中方括号部分表示已经被排除的数。
+\`\`\`math
+A: 1 3 4 9
+     ↑
+B: [1 2 3] 4 5 6 7 8 9
+             ↑
+\`\`\`
+由于 A[1]<B[4]，因此排除 A[0] 到 A[1]，即数组 A 的下标偏移变为 2，同时更新 k 的值：k=k−k/2=2。
+
+下一步寻找，比较两个有序数组中下标为 k/2−1=0 的数，即比较 A[2] 和 B[3]，如下面所示，其中方括号部分表示已经被排除的数。
+\`\`\`math
+A: [1 3] 4 9
+         ↑
+B: [1 2 3] 4 5 6 7 8 9
+           ↑
+\`\`\`
+由于 A[2]=B[3]，根据之前的规则，排除 A 中的元素，因此排除 A[2]，即数组 A 的下标偏移变为 3，同时更新 k 的值： k=k−k/2=1。
+
+由于 k 的值变成 1，因此比较两个有序数组中的未排除下标范围内的第一个数，其中较小的数即为第 k 个数，由于 A[3]>B[3]，因此第 k 个数是 B[3]=4。
+\`\`\`math
+A: [1 3 4] 9
+           ↑
+B: [1 2 3] 4 5 6 7 8 9
+           ↑
+\`\`\`
+### 代码
+
+\`\`\`c showLineNumbers
+int solve(int* A, int aStart, int aEnd, int* B, int bStart, int bEnd, int k) {
+    // If the segment of on array is empty, it means we have passed all
+    // its element, just return the corresponding element in the other array.
+    if (aEnd < aStart) {
+        return B[k - aStart];
+    }
+    if (bEnd < bStart) {
+        return A[k - bStart];
+    }
+
+    // Get the middle indexes and middle values of A and B.
+    int aIndex = (aStart + aEnd) / 2, bIndex = (bStart + bEnd) / 2;
+    int aValue = A[aIndex], bValue = B[bIndex];
+
+    // If k is in the right half of A + B, remove the smaller left half.
+    if (aIndex + bIndex < k) {
+        if (aValue > bValue) {
+            return solve(A, aStart, aEnd, B, bIndex + 1, bEnd, k);
+        } else {
+            return solve(A, aIndex + 1, aEnd, B, bStart, bEnd, k);
+        }
+    }
+    // Otherwise, remove the larger right half.
+    else {
+        if (aValue > bValue) {
+            return solve(A, aStart, aIndex - 1, B, bStart, bEnd, k);
+        } else {
+            return solve(A, aStart, aEnd, B, bStart, bIndex - 1, k);
+        }
+    }
+}
+
+double findMedianSortedArrays(int* A, int na, int* B, int nb) {
+    int n = na + nb;
+    if (n % 2 == 1) {
+        return solve(A, 0, na - 1, B, 0, nb - 1, n / 2);
+    } else {
+        return (solve(A, 0, na - 1, B, 0, nb - 1, n / 2) +
+                solve(A, 0, na - 1, B, 0, nb - 1, n / 2 - 1)) /
+               2.0;
+    }
+}
+\`\`\`
+
+### 复杂度分析
+
+Let $m$ be the size of array \`nums1\` and $n$ be the size of array \`nums2\`.
+
+- **时间复杂度:** $O(log(m+n))$
+
+  - 其中 m 和 n 分别是数组 nums 1​和 nums 2​的长度。初始时有 $k=(m+n)/2$ 或 $k=(m+n)/2+1$，每一轮循环可以将查找范围减少一半，因此时间复杂度是 $O(log(m+n))$。
+
+- **空间复杂度:** $O(1)$
+
+`,
+                    difficulty: "HARD",
+                    published: true,
+                    templates: {
+                        create: [
+                            {
+                                language: "c",
+                                template: `
+#include <stdio.h>
+#include <stdlib.h>
+#include <string.h>
+
+// 解析输入数组
+int *parseIntArray(char *line, int *len) {
+    line[strcspn(line, "\\n")] = 0; // 移除换行符
+    char *p = line;
+    while (*p && (*p == '[' || *p == ' ' || *p == ']')) p++; // 跳过空格和括号
+
+    int capacity = 10;
+    int *arr = malloc(capacity * sizeof(int)); // 初始分配空间
+    *len = 0;
+
+    char *token = strtok(p, ","); // 分割输入为逗号分隔的整数
+    while (token) {
+        if (*len >= capacity) { // 扩展数组大小
+            capacity *= 2;
+            arr = realloc(arr, capacity * sizeof(int));
+        }
+        arr[(*len)++] = atoi(token); // 存储整数
+        token = strtok(NULL, ",");
+    }
+    return arr;
+}
+
+double findMedianSortedArrays(int* nums1, int nums1Size, int* nums2, int nums2Size);
+
+int main() {
+    char line[1024];
+
+    while (fgets(line, sizeof(line), stdin)) { // 读取第一行
+        int len1;
+        int *nums1 = parseIntArray(line, &len1); // 解析数组1
+
+        if (!fgets(line, sizeof(line), stdin)) break; // 如果第二行不存在，退出
+        int len2;
+        int *nums2 = parseIntArray(line, &len2); // 解析数组2
+
+        double result = findMedianSortedArrays(nums1, len1, nums2, len2); // 计算中位数
+        printf("%.5f\\n", result); // 输出中位数，保留5位小数
+
+        free(nums1); // 释放内存
+        free(nums2); // 释放内存
+    }
+
+    return 0;
+}
+
+
+// 寻找中位数函数 
+double findMedianSortedArrays(int* nums1, int nums1Size, int* nums2, int nums2Size) {
+    
+    return 0.0; // 在这里填充你的算法逻辑
+}
+`,
+                            },
+                            {
+                                language: "cpp",
+                                template: `
+#include <iostream>
+#include <vector>
+#include <string>
+#include <sstream>
+#include <algorithm>
+using namespace std;
+
+class Solution {
+public:
+    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2);
+};
+
+// 解析输入为整数数组
+vector<int> parseIntArray(const string& line) {
+    string trimmed = line;
+    trimmed.erase(remove(trimmed.begin(), trimmed.end(), '['), trimmed.end());
+    trimmed.erase(remove(trimmed.begin(), trimmed.end(), ']'), trimmed.end());
+
+    vector<int> result;
+    stringstream ss(trimmed);
+    string token;
+    while (getline(ss, token, ',')) {
+        if (!token.empty()) {
+            result.push_back(stoi(token));
+        }
+    }
+    return result;
+}
+
+int main() {
+    string line;
+    while (getline(cin, line)) {
+        vector<int> nums1 = parseIntArray(line);
+        if (!getline(cin, line)) break;
+        vector<int> nums2 = parseIntArray(line);
+
+        Solution sol;
+        double result = sol.findMedianSortedArrays(nums1, nums2);
+        printf("%.5f\\n", result);
+    }
+    return 0;
+}
+
+
+
+double Solution::findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
+
+    return 0.0; // 临时返回值，待填充
+}
+`,
+                            },
+                        ],
+                    },
+                    testcases: {
+                        create: [
+                            {
+                                data: {
+                                    create: [
+                                        { label: "nums1", value: "[1,3]", index: 0 },
+                                        { label: "nums2", value: "[2]", index: 1 },
+                                    ],
+                                },
+                                expectedOutput: "2.00000",
+                            },
+                            {
+                                data: {
+                                    create: [
+                                        { label: "nums1", value: "[1,2]", index: 0 },
+                                        { label: "nums2", value: "[3,4]", index: 1 },
+                                    ],
+                                },
+                                expectedOutput: "2.50000",
+                            },
+                        ],
+                    },
+                },
+            ],
+        },
+    },
+];
+
+export async function main() {
+    for (const e of editorLanguageConfigData) {
+        await prisma.editorLanguageConfig.create({ data: e });
+    }
+
+    for (const u of userData) {
+        await prisma.user.create({ data: u });
+    }
+}
+
+main();